Inventions and Deceptions – Hill Sphere

The Hill Sphere is defined by Wikipedia as:

An astronomical body’s Hill Sphere is the region in which it dominates the attraction of satellites. To be retained by a planet, a moon must have an orbit that lies within the planet’s Hill sphere. That moon would, in turn, have a Hill sphere of its own. Any object within that distance would tend to become a satellite of the moon, rather than of the planet itself.

In more precise terms, the Hill sphere approximates the gravitational sphere of influence of a smaller body in the face of perturbations from a more massive body.

It was defined by the American astronomer George William Hill, based upon the work of the French astronomer Édouard Roche. For this reason, it is also known as the Roche sphere (not to be confused with the Roche limit).

The Hill sphere extends between the Lagrangian points L1 and L2, which lie along the line of centers of the two bodies. The region of influence of the second body is shortest in that direction, and so it acts as the limiting factor for the size of the Hill sphere. Beyond that distance, a third object in orbit around the second (e.g. Jupiter) would spend at least part of its orbit outside the Hill sphere, and would be progressively perturbed by the tidal forces of the central body (e.g. the Sun), eventually ending up orbiting the latter.

A contour plot of the effective potential of a two-body system
due to gravity and inertia at one point in time.
The Hill spheres are the circular regions surrounding the two large masses.
(Earth and sun radii are not drawn to scale.)

http://en.wikipedia.org/wiki/Hill_sphere

George William Hill was a very smart astronomer and mathematician who described a two-body problem where “the gravitational sphere of influence of one astronomical body in the face of perturbations from another heavier body around which it orbits”

George William Hill (March 3, 1838 – April 16, 1914) was an American astronomer and mathematician.

Hill was born in New York City, New York to painter and engraver John William Hill and Catherine Smith Hill. He moved to West Nyack with his family when he was eight years old. After attending high school, Hill graduated from Rutgers University in 1859.

In 1861 he was hired by John Daniel Runkle[1] at the Nautical Almanac Office in Cambridge, Massachusetts. His work focused on the mathematics describing the three-body problem, later the four-body problem, to calculate the orbits of the Moon around the Earth, as well as that of planets around the Sun.

The Hill sphere, which approximates the gravitational sphere of influence of one astronomical body in the face of perturbations from another heavier body around which it orbits, was described by Hill.

He became president of the American Mathematical Society in 1894, serving for two years. He was elected to the Royal Society of Edinburgh in 1908, as well as to the academies of Belgium (1909), Christiania (1910), Sweden (1913), among others.

http://en.wikipedia.org/wiki/George_William_Hill

Unfortunately, modern post-normal science has inappropriately deployed George William Hill’s description of the two-body problem to explain the gravitational dynamics of three-body systems; such as the Sun-Earth-Moon system.

The Wikipedia illustration attempts to finesse the inappropriate combination of two two-body systems [Sun-Earth and Earth-Moon] into a three-body Sun-Earth-Moon system.

However, the planetary configuration at New Moon clearly illustrates:
1) A theoretical two-body solution cannot be applied to a real three-body situation.
2) The failure of Newtonian Gravity to explain the orbits of the Earth and Moon.

The Earth orbits the Sun.

The Moon orbits the Sun [with some perturbations caused by the Earth].

The Earth and Moon have equal orbital velocities [around the Sun] at the New Moon alignment of about 29.78 km/s [the average orbital speed of the Earth].

The Sun’s gravitational attraction on the Moon overpowers the Earth’s gravitational attraction on the Moon by a factor of two [see the University of Saskatchewan calculation below].

Therefore, according to Newtonian Gravity, the Moon [after New Moon] should adopt a regular orbit around the Sun. The Moon cannot orbit the Earth because the Earth cannot overpower the Sun’s gravitational attraction on the Moon.

The University of Saskatchewan [see below] manages to creatively avoid the mathematical consequences of Newtonian Gravity in a three-body situation by deploying the two-body Hill Sphere finesse: “The Sun has captured the whole Earth-Moon system”.

The impossibility of the Moon’s orbit [according to Newtonian Gravity] was highlighted back in 1979 by Walter C Wright in his book “Gravity is a Push”:
“My conclusion is that the sun and the earth have no pull factor on the moon”

Ralph Rene similarly concluded that Newtonian Gravity was “impossible” in his 1998 book “The Last Skeptic of Science”:

Miles Mathis reviewed the work of Ralph Rene and concluded: “Mr. René is correct”.

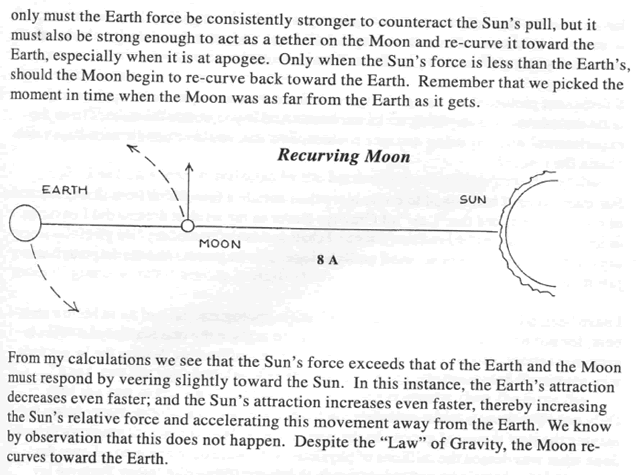
I think we must see that he is correct. We have a real problem here, and the standard-model answer is just one more pathetic dodge.
… … … …
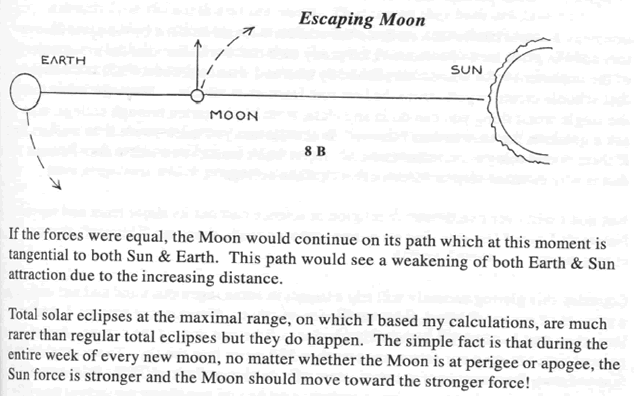
Mr. René is correct. Even if the Moon and Earth could theoretically inhabit the same orbit, the Moon would have to be pulled lower at New Moon by the Sun. If it were, it could not re-establish its original distance. Once its distance from the Earth had been increased, its pull from the Earth would be lessened, due to the same equation. It would escape very quickly.

Another Hole in Celestial Mechanics
Miles Mathis
http://milesmathis.com/cm2.html