Trawling through the mainstream documentation it becomes apparent that Earth Scientists have to operate in a bi-polar world where there is one set of Settled Science covering the Earth’s Crust and another set of Settled Science governing the Earth’s Mantle and Core.
It also appears that the Amalgamated Union of Earth Scientists have established a demarcation line between these bi-polar sets of Settled Science called the Mohorovičić Discontinuity [aka Moho] which mustn’t be crossed by union members.
The Mohorovičić discontinuity, usually referred to as the Moho, is the boundary between the Earth’s crust and the mantle.
…
The Mohorovičić discontinuity is 5 to 10 kilometres (3–6 mi) below the ocean floor, and 20 to 90 kilometres (10–60 mi), with an average of 35 kilometres (22 mi), beneath typical continents.https://en.wikipedia.org/wiki/Mohorovi%C4%8Di%C4%87_discontinuity
Imaging the mantle beneath Iceland using integrated seismological techniques
Richard M. Allen, Guust Nolet, W. Jason Morgan, Kristin Vogfjord, Bergur H. Bergsson, Palmi Erlendsson, G. R. Foulger, Steinunn Jakobsdottir, Bruce R. Julian, Matt Pritchard, Sturla Ragnarsson, and Ragnar Stefansson
Journal of Geophysical Research, Vol. 107, No. B12, 2325, 2002
The Wikipedia illustration of the Mohorovičić Discontinuity demarcation line provides a fairly simple overview where the P Waves are represented by one [unexpectedly strange] straight line and one [as expected] curved line.
Two paths of a P-wave, one direct and one refracted as it crosses the Moho.
https://en.wikipedia.org/wiki/Mohorovi%C4%8Di%C4%87_discontinuity
A more detailed explanation of the Mohorovičić Discontinuity [and the pioneering work of Andrija Mohorovičić] is available at the Andrija Mohorovičić’s Memorial Rooms website.
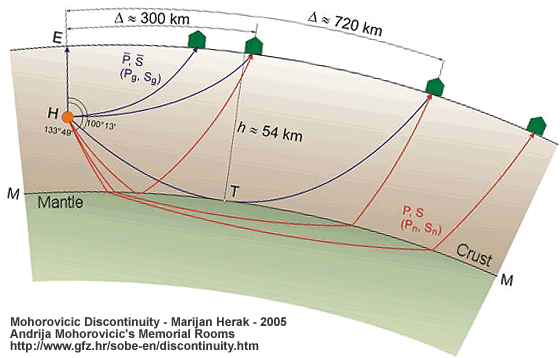
The smooth increase of velocity with depth is assumed valid in both media, but on the boundary surface seismic wave velocities suddenly increase.
Mohorovičić distinguished “individual” waves ( P, S, nowadays called Pg, Sg), whose rays lie only in the crust, and “normal” waves (P, S – nowadays known as Pn, Sn) whose rays enter the mantle and are then refracted back towards the surface of the Earth.
Mohorovičić Discontinuity – Marijan Herak – 2005
Andrija Mohorovičić’s Memorial Rooms
http://www.gfz.hr/sobe-en/discontinuity.htm
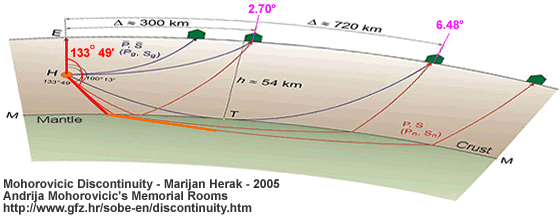
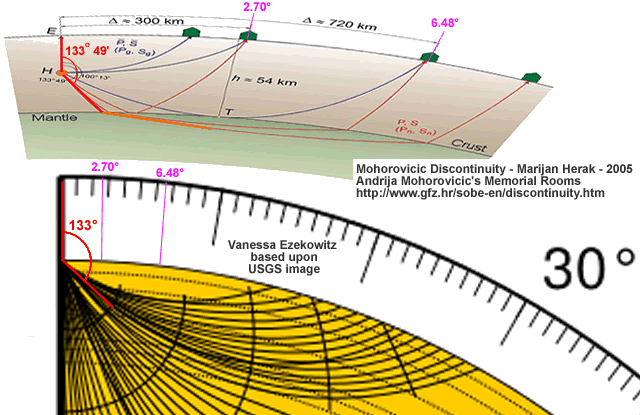
Rescaling the published image so that it [fairly] accurately reflects the 133° 49’ angle displayed in the text it becomes apparent that the refraction in the illustration appears to be unrealistically sharp if [as shown by Wikipedia] there is only an average speed difference of 1 kilometre per second between the P Waves that cross the Mohorovičić Discontinuity and those that don’t cross this demarcation line.
Revisiting the work of Mohorovičić we find he proposed that “the wave velocity increases with depth” according to an exponential function so that seismic waves are “smooth concave curves” and that these smooth concave curves “succeeded in answering all the questions he posed to himself regarding the propagation of seismic waves.”
Mohorovičić Discontinuity – Marijan Herak – 2005
Andrija Mohorovičić’s Memorial Rooms
http://www.gfz.hr/sobe-en/discontinuity.htm
In other words: Mohorovičić was not a member of the Amalgamated Union of Earth Scientists and he did not propose [or require] the Mohorovičić Discontinuity but he did observe that some seismic waves were being reflected from a depth of 54 kilometres.
Discovering there were reflections from a depth of 54 kilometres during the Kupa Valley earthquake of 8 October 1909 is not the same as discovering a worldwide discontinuity.
His train of thought closely follows Feynman’s (1967) “recipe” for the creation of a new physical law – guess it, compute consequences, compare them to nature and observations, if they agree it is right, if they disagree it is wrong (paraphrased).
This trial-and-error approach is even today often the method of choice in solving inverse problems, one of the first of which in seismology was solved by Mohorovičić in 1910.
There are also other, less-known achievements of his, including
an elegant method of location of epicenters (Mohorovičić’s epicentrals, 1915–1918),
a method to determine total friction in mechanical seismographs (1917, 1918, 1924),
a novel seismograph design (1917, 1918, unfortunately never realized),
a number of improved travel-time curves (1914a, b, c), etc.
Mohorovičić was also among the first to recognize the importance of the seismic-resistant design of buildings.
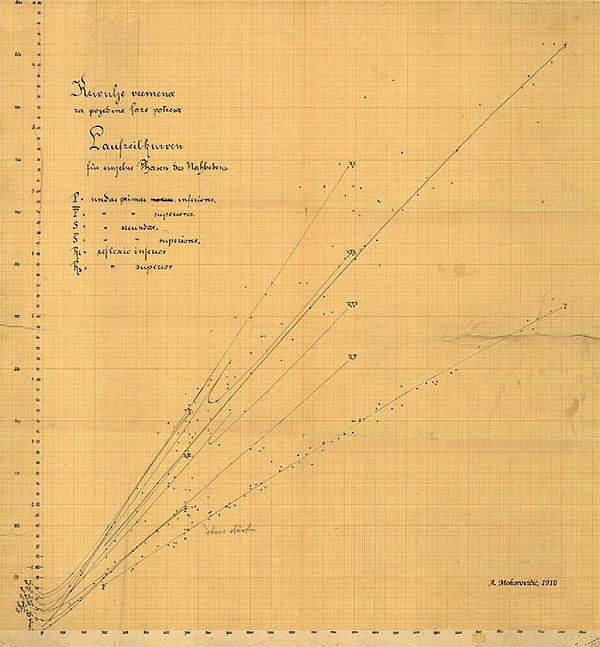
Mohorovičić’s travel-time curves for local and regional distances from 1910.
Observed onset times are marked with dots, full lines are the theoretical travel-time curves for individual (Pg, Sg) and normal (Pn, Sn) phases, as well as for the main crustal reflections for the best-fitting model of the crust and the upper mantle.
Andrija Mohorovičić (1857–1936 – On the occasion of the 150th anniversary of his birth
Davorka Herak and Marijan Herak – Historical Seismologist – November/December 2007
http://www.seismosoc.org/publications/SRL/SRL_78/srl_78-6_hs.html
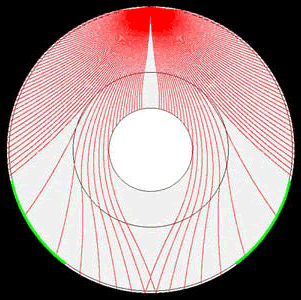
Unsurprisingly, the Amalgamated Union of Earth Scientists clearly requires [see image below] that seismic waves express “smooth concave curves” when they are travelling large distances through the crust, mantle or core.
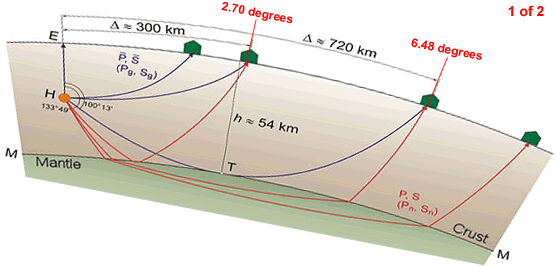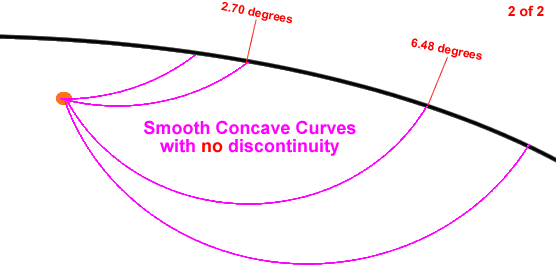
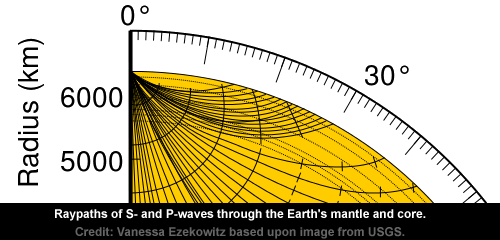
It is very interesting to note that the global raypath diagram used by Wikipedia manages to totally overlook the seismic waves that are meant to be significantly refracted by the Mohorovičić Discontinuity close to the epicentre and it only depicts seismic waves surfacing at about 14°.
Even more telling is the fact that the global raypaths up to an angle of 133° 49’ contradict the raypaths used in the detailed illustration of the Mohorovičić Discontinuity.
Therefore, the Mohorovičić Discontinuity is purely a fictional device invented by the Amalgamated Union of Earth Scientists.
Furthermore, without this fictitious demarcation line it is evident that the Earth’s crust is typically hundreds of kilometres thick and the continental crust is not “30 km (20 mi) to 50 km (30 mi) thick” as proposed by the Amalgamated Union of Earth Scientists.
The oceanic crust is 5 km (3 mi) to 10 km (6 mi) thick and is composed primarily of basalt, diabase, and gabbro.
The continental crust is typically from 30 km (20 mi) to 50 km (30 mi) thick and is mostly composed of slightly less dense rocks than those of the oceanic crust.
Interestingly, these “smooth concave curves” raypaths in a thick crust [hundreds of kilometres deep] appear to be fully compatible with Jan Lamprecht’s model of the Earth’s interior which has a cavity [instead of a core] and where the mantle density decreases beyond a certain depth.
Hollow Planet Seismology vs Solid Earth Seismology – Jan Lamprecht
http://www.bibliotecapleyades.net/tierra_hueca/esp_tierra_hueca_9.htm?sa=X&ved=0CBgQ9QEwATgUahUKEwjg2ezcuvnGAhVDaxQKHdy4Des
UPDATE 13 August 2015
Having managed to locate the English translation of Earthquake of 8 October 1909 by Andrija Mohorovičić it is possible to definitively verify that the Amalgamated Union of Earth Scientists are misrepresenting the thoughts of Andrija Mohorovičić.
Specifically, Mohorovičić saw “the Earth as a solid body composed of concentric homogeneous spherical layers” and he thought “the velocity of propagation increases from the surface down to a significant depth”.
The problem of earthquake wave propagation has been solved in general.
If we imagine the Earth as a solid body composed of concentric homogeneous spherical layers, every sudden change of equilibrium will, regardless if it occurs at the surface of the Earth or at any point in the interior, cause two systems of elastic waves which propagate with different velocities from the earthquake focus in all directions.
Because the velocity of propagation increases from the surface down to a significant depth, so the path of every impact from the focus to the Earth surface will be an upward concave curve.
In the same way every ray reaching the surface of the Earth will cause various new systems of waves of which some will further extend along the surface and the others will reflect towards the interior of the Earth.
If in the interior of the Earth there exists a spherical surface as a dividing interface between two media with different elasticity, then new wave systems will be generated at that surface due to refraction and reflection.
Click to access Mohorovicic.pdf







Post updated – see above.
Having located the English translation of Earthquake of 8 October 1909 by Andrija Mohorovičić it is possible to definitively verify his thoughts.