There are finite limits on the knowledge of Earth Scientists.
For example, the deepest borehole drilled into the Earth only reached a depth of 12,262 metres.
The Kola Superdeep Borehole is the result of a scientific drilling project of the Soviet Union in the Pechengsky District, on the Kola Peninsula, longitude and latitude coordinate: 69°23’46″N 30°36’32″E.
The project attempted to drill as deep as possible into the Earth’s crust.
Drilling began on 24 May 1970 using the Uralmash-4E, and later the Uralmash-15000 series drilling rig.
A number of boreholes were drilled by branching from a central hole.
The deepest, SG-3, reached 12,262 metres (40,230 ft) in 1989 and still is the deepest artificial point on Earth.
In terms of true depth, it is the deepest borehole in the world.
In other words: Earth Scientists have some knowledge of the Earth down to 0.19% of the distance to the centre of the Earth [at one location] and no direct knowledge of the other 99.81%.
Mean radius 6371.0 km
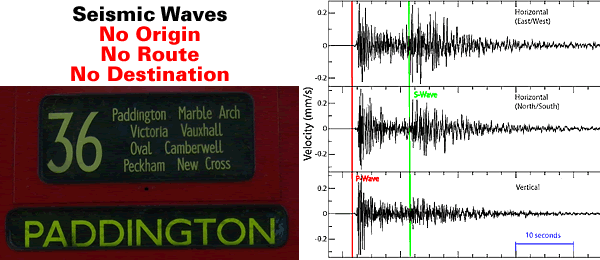
Another example of the finite limits placed upon the knowledge of Earth Scientists is that the seismic waves they detect do not contain neatly labelled metadata which clearly annotates their point[s] of origin, their final destination[s] or their routing information.
However, Earth Scientists have slowly developed an understanding of seismic waves.
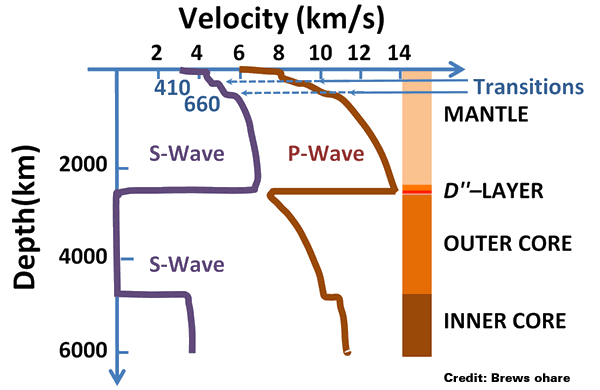
Primary waves (P-waves) are compressional waves that are longitudinal in nature. P waves are pressure waves that travel faster than other waves through the earth to arrive at seismograph stations first, hence the name “Primary”.
These waves can travel through any type of material, including fluids, and can travel at nearly twice the speed of S waves.
In air, they take the form of sound waves, hence they travel at the speed of sound.
Typical speeds are 330 m/s in air, 1450 m/s in water and about 5000 m/s in granite.Secondary waves (S-waves) are shear waves that are transverse in nature. Following an earthquake event, S-waves arrive at seismograph stations after the faster-moving P-waves and displace the ground perpendicular to the direction of propagation. Depending on the propagational direction, the wave can take on different surface characteristics; for example, in the case of horizontally polarized S waves, the ground moves alternately to one side and then the other.
S-waves can travel only through solids, as fluids (liquids and gases) do not support shear stresses.
S-waves are slower than P-waves, and speeds are typically around 60% of that of P-waves in any given material.Rayleigh waves, also called ground roll, are surface waves that travel as ripples with motions that are similar to those of waves on the surface of water (note, however, that the associated particle motion at shallow depths is retrograde, and that the restoring force in Rayleigh and in other seismic waves is elastic, not gravitational as for water waves).
The existence of these waves was predicted by John William Strutt, Lord Rayleigh, in 1885. They are slower than body waves, roughly 90% of the velocity of S waves for typical homogeneous elastic media.
In the layered medium (like the crust and upper mantle) the velocity of the Rayleigh waves depends on their frequency and wavelength.Love waves are horizontally polarized shear waves (SH waves), existing only in the presence of a semi-infinite medium overlain by an upper layer of finite thickness.
They are named after A.E.H. Love, a British mathematician who created a mathematical model of the waves in 1911.
They usually travel slightly faster than Rayleigh waves, about 90% of the S wave velocity, and have the largest amplitude.A Stoneley wave is a type of boundary wave (or interface wave) that propagates along a solid-fluid boundary or, under specific conditions, also along a solid-solid boundary. Amplitudes of Stoneley waves have their maximum values at the boundary between the two contacting media and decay exponentially towards the depth of each of them.
These waves can be generated along the walls of a fluid-filled borehole, being an important source of coherent noise in VSPs and making up the low frequency component of the source in sonic logging.
The equation for Stoneley waves was first given by Dr. Robert Stoneley (1894 – 1976), Emeritus Professor of Seismology, Cambridge.Free Oscillations of the Earth
This phenomenon is a result of interference between two surface waves traveling in opposite directions.
In fact it is a surface standing wave.
Interference of Rayleigh waves results in spheroidal oscillation S while interference of Love waves gives toroidal oscillation T.
The first observations of free oscillations of the Earth were done during the great 1960 earthquake in Chile.
Their knowledge of seismic waves has enabled Earth Scientists to develop triangulation techniques and “guess and correction” algorithms to locate the origin of seismic waves.
In the case of local or nearby earthquakes, the difference in the arrival times of the P and S waves can be used to determine the distance to the event.
In the case of earthquakes that have occurred at global distances, three or more geographically diverse observing stations (using a common clock) recording P-wave arrivals permits the computation of a unique time and location on the planet for the event.
Typically, dozens or even hundreds of P-wave arrivals are used to calculate hypocenters.
The misfit generated by a hypocenter calculation is known as “the residual”.
Residuals of 0.5 second or less are typical for distant events, residuals of 0.1-0.2 s typical for local events, meaning most reported P arrivals fit the computed hypocenter that well.
Typically a location program will start by assuming the event occurred at a depth of about 33 km; then it minimizes the residual by adjusting depth.
Most events occur at depths shallower than about 40 km, but some occur as deep as 700 km.
A quick way to determine the distance from a location to the origin of a seismic wave less than 200 km away is to take the difference in arrival time of the P wave and the S wave in seconds and multiply by 8 kilometers per second.
Modern seismic arrays use more complicated earthquake location techniques.
https://en.wikipedia.org/wiki/Seismic_wave
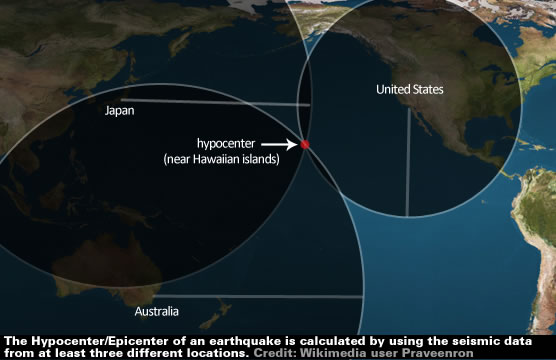
One seismograph would give the distance, but that could be plotted as a circle, with an infinite number of possibilities.
Two seismographs would give two intersecting circles, with two possible locations.
Only with a third seismograph would there be a precise location.
The process of accurate location, was greatly improved with the advent of precise absolute timing.
Early seismographs were almost always located at an astronomical observatory, just for the purpose of timing.
Recently, GPS is being used for accurate time, and seismometers can be located almost anywhere.
Modern earthquake location still requires a minimum of three seismometers.
Most likely, there are many, forming a seismic array.
The emphasis is on precision, since much can be learned about the fault mechanics and seismic hazard, if the locations can be determined to within a kilometer or two, for small earthquakes.
For this, computer programs use an iterative process, involving a ‘guess and correction’ algorithm.
As well, a very good model of the local crustal velocity structure is required: seismic velocities vary with the local geology.
For P-waves, the relation between velocity and bulk density of the medium has been quantified in Gardner’s relation.
https://en.wikipedia.org/wiki/Seismic_wave
In trigonometry and geometry, triangulation is the process of determining the location of a point by measuring angles to it from known points at either end of a fixed baseline, rather than measuring distances to the point directly (trilateration).
The point can then be fixed as the third point of a triangle with one known side and two known angles.
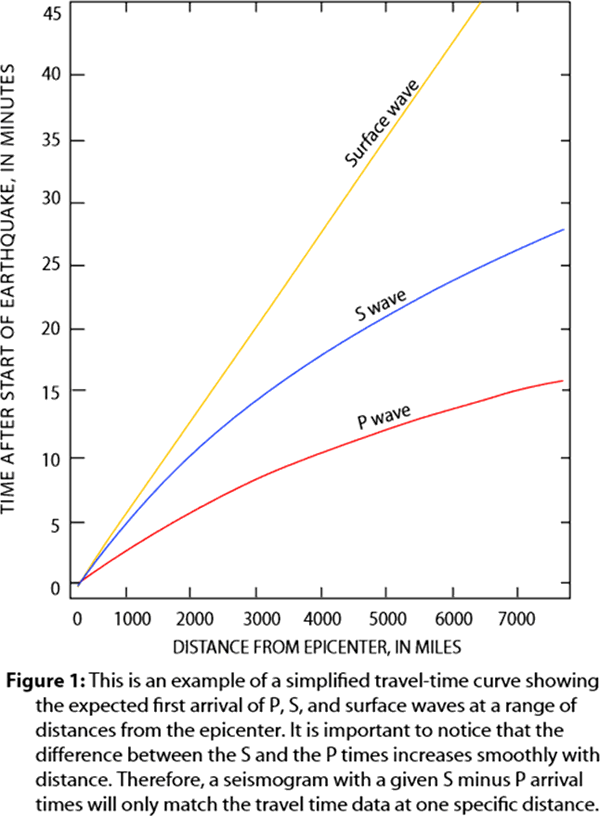
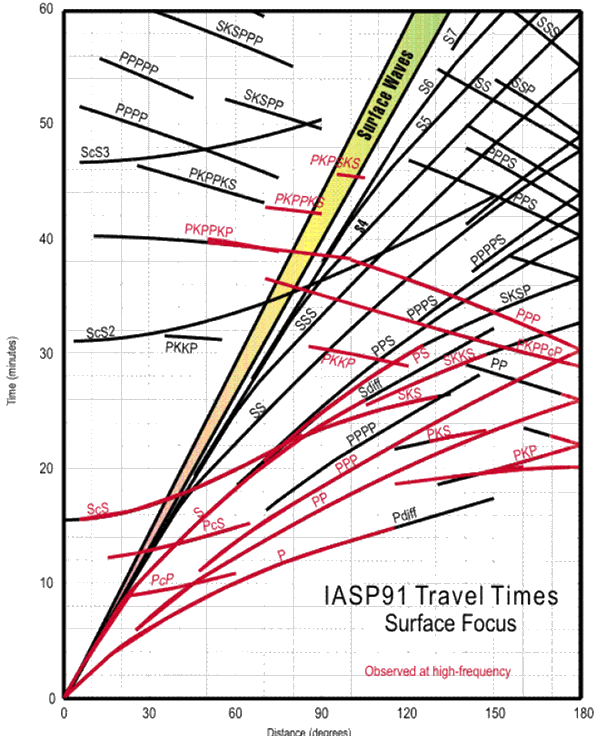
This knowledge has been simplified into a ready reckoner for quickly locating earthquakes.
The curves are the result of analyzing seismic waves from thousands of earthquakes, received by hundreds of seismic stations around the world.
They are used by seismologists to quickly locate earthquakes.
IRIS – Incorporated Research Institutions for Seismology
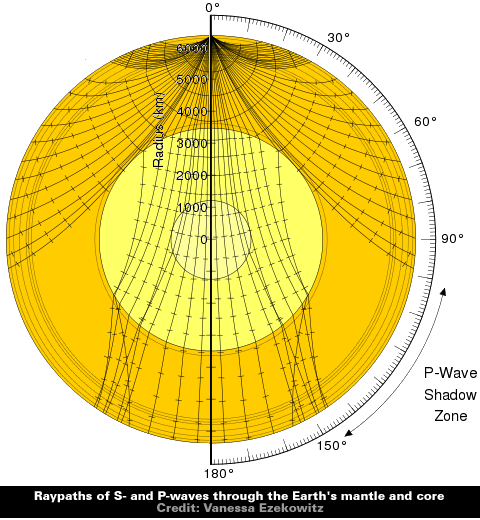
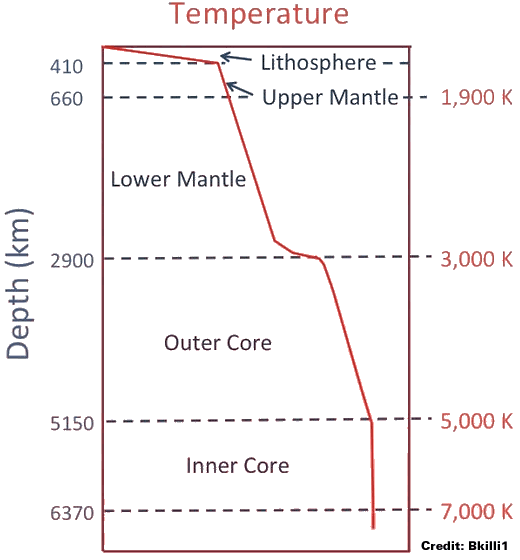
The overall picture becomes far more complicated for the Earth Scientists when they consider seismic waves that are deemed to have been reflected or refracted by changes in density and stiffness [which “vary according to temperature, composition and phase”] as they travelled through the interior of the Earth.
Body waves travel through the interior of the Earth.
They create raypaths refracted by the varying density and modulus (stiffness) of the Earth’s interior.
The density and modulus, in turn, vary according to temperature, composition, and phase.
This effect resembles the refraction of light waves.
However, these problematic body waves are used by the ever inventive Earth Scientists to develop an internal model of the Earth and a series of raypaths for these reflected or refracted seismic waves based upon their 99.81% ignorance of the internal structure of the Earth, a handful of rules and Consensus Settled Science.
The propagation velocity of the waves depends on density and elasticity of the medium.
Velocity tends to increase with depth and ranges from approximately 2 to 8 km/s in the Earth’s crust, up to 13 km/s in the deep mantle.
…
Primary waves can travel through any type of material, including fluids, and can travel at nearly twice the speed of S waves.
…
S-waves can travel only through solids, as fluids (liquids and gases) do not support shear stresses.https://en.wikipedia.org/wiki/Seismic_wave
when a P-wave strikes the boundary of molten and solid cores, S-waves will then propagate in the solid medium.
And when the S-waves hit the boundary again they will in turn create P-waves.
…
When an S- or P-wave strikes an interface at an angle other than 90 degrees, a phenomenon known as mode conversion occurs.As described above, if the interface is between a solid and liquid, S becomes P or vice versa.
However, even if the interface is between two solid media, mode conversion results.
If a P-wave strikes an interface, four propagation modes may result: reflected and transmitted P and reflected and transmitted SV.
Similarly, if an SV-wave strikes an interface, the same four modes occur in different proportions.
The inventiveness of the Earth Scientists is constrained by the needs of other disciplines within the Earth Sciences such as plate tectonics, geomagnetism and volcanism.
Nonetheless, the Earth Scientists have [somehow] transformed their 99.81% ignorance of the Earth’s interior into Settled Science.
https://en.wikipedia.org/wiki/Earth
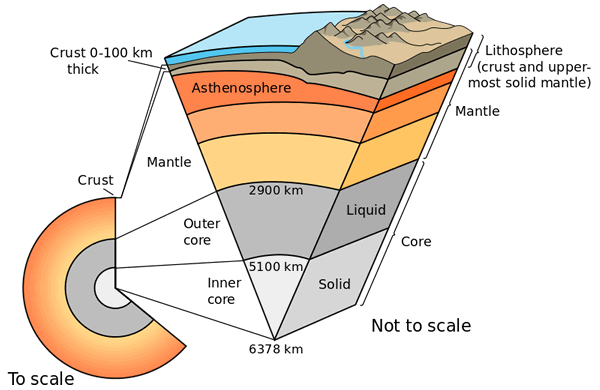
https://en.wikipedia.org/wiki/Structure_of_the_Earth
https://en.wikipedia.org/wiki/P-Wave
https://en.wikipedia.org/wiki/Geothermal_gradient
Basalt has high liquidus and solidus temperatures – values at the Earth’s surface are near or above 1200 °C (liquidus) and near or below 1000 °C (solidus); these values are higher than those of other common igneous rocks.
The Earth Scientists are so enamoured with their model that they have created concatenated codes to identify their raypaths and even assigned travel times for these reflected and refracted seismic waves.
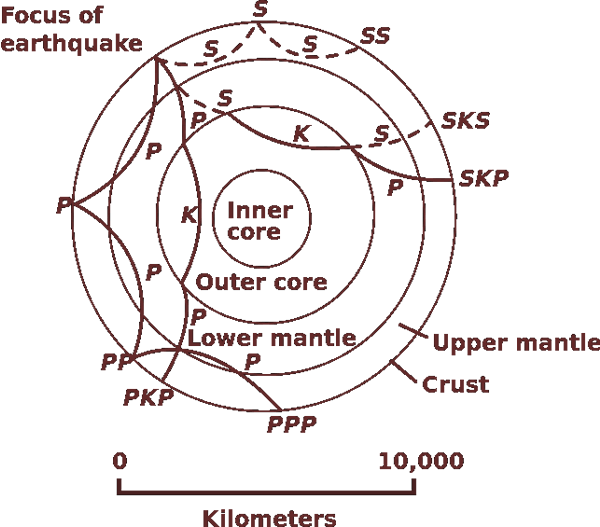
Cross section of the whole Earth, showing the complexity of paths of earthquake waves.
The paths curve because the different rock types found at different depths change the speed at which the waves travel.
Solid lines marked P are compressional waves; dashed lines marked S are shear waves.
S waves do not travel through the core but may be converted to compressional waves (marked K) on entering the core (PKP, SKS).
Waves may be reflected at the surface (PP, PPP, SS).
https://en.wikipedia.org/wiki/Seismic_wave
IRIS – Incorporated Research Institutions for Seismology
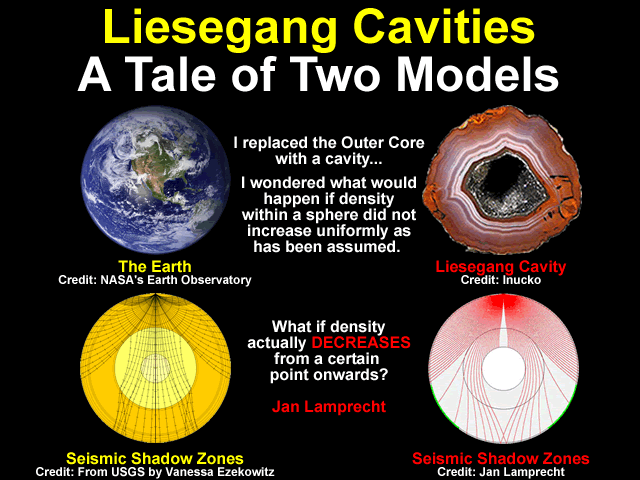
The first hint that there may be a problem with the Earth Scientists ability to transform their 99.81% ignorance of the Earth’s interior into Settled Science arrived when the modelling undertaken by Jan Lamprecht revealed a model [“which made seismic sense”] of the Earth’s interior with a cavity [instead of a core] and a mantle where the density
starts to decrease beyond a certain depth.
When I did my feasibility study (which is what my book is), I looked at the problem from every conceivable angle to see if there was any Hollow Earth model which made seismic sense.
I found only one – I repeat – only one, which has any merits.
…
In the above model, I simply used the Earth’s structure as scientists define it now.I replaced the Outer Core with a cavity
(I’ll explain why later – because there is a sound reason for it).But the thing I changed was the structure of the Mantle.
I wondered what would happen if density within a sphere did not increase uniformly as has been assumed.
What if density actually DECREASES from a certain point onwards?
Hollow Planet Seismology vs Solid Earth Seismology – Jan Lamprecht
http://www.bibliotecapleyades.net/tierra_hueca/esp_tierra_hueca_9.htm?sa=X&ved=0CBgQ9QEwATgUahUKEwjg2ezcuvnGAhVDaxQKHdy4Des
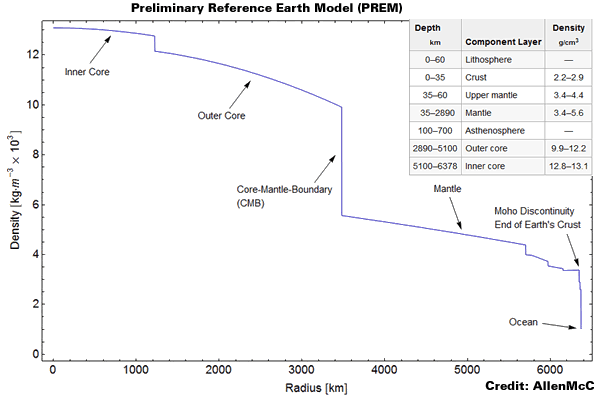
The second hint that there may be a problem with the Earth Scientists ability to transform their 99.81% ignorance of the Earth’s interior into Settled Science arrived when it was realised that seismic waves deemed to have passed through the dense Core “actually slow down”.
It has long been known to scientists that unlike P waves which can travel around the world – S waves are in fact “blocked” by something.
They named this “something” the Outer Core.
They decided the Outer Core had to be non-rigid.
If the Outer Core were a type of “liquid” then P waves could pass through it, but S waves could not.
Hence they “invented” the Outer Core.
Very early on, when I became interested in the Hollow Earth idea, I realized this property of the Outer Core, and I wondered if the Outer Core was really a liquid, or if it was, in reality a cavity.
…
The waves we are interested in are those which passed through the core – the PKP and PKIKP waves.When one takes a look at the data showing the speed with which seismic waves travel, one discovers an interesting thing: Waves which pass through the Core (those which are supposed to be going in a straight line) actually slow down!
What makes this even more curious is that P waves are supposed to speed up when they pass through dense material.
And there is no place on this planet which is as dense as the Inner Core!
So why do P waves then slow down? According to the formula for the transmission of sound/pressure waves – speed is affected by two factors: (a) Density (b) Elasticity.
This gives scientists a way of getting out of the problem by saying: “If the Density has increased, but the wave has slowed down, it must THEREFORE mean that the Elasticity increased.”
Hollow Planet Seismology vs Solid Earth Seismology – Jan Lamprecht
http://www.bibliotecapleyades.net/tierra_hueca/esp_tierra_hueca_9.htm?sa=X&ved=0CBgQ9QEwATgUahUKEwjg2ezcuvnGAhVDaxQKHdy4Des
The third hint that there may be a problem with the Earth Scientists ability to transform their 99.81% ignorance of the Earth’s interior into Settled Science arrived when it was realised that earthquakes occur in the “highly viscous, mechanically weak and ductilely deforming” asthenosphere and that the occurrence of earthquakes increases after a depth of 400 kilometres [where there Earth is meant to be increasingly hot and increasingly viscous] until they disappear at a depth of around 700 kilometres.
According to scientists, pressure increases with depth.
According to their calculations the pressure is so great that between 70-150 Km down, all rock will begin to flow.
Below 150 Km there is no known material which will not flow.
Therefore, according to scientists, there can be no earthquakes with epicenters deeper than 150 Km – because it is IMPOSSIBLE!
But there are!
Tens of thousands of Earthquakes have epicenters deeper than 150 Km.
The histogram below shows some curious things.
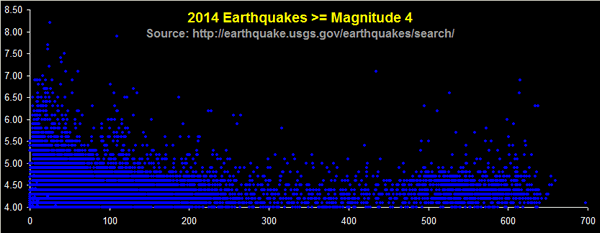
It shows that earthquakes occur right up to a depth of 300 Km down.
…
Then a most curious thing happens, they increase in number up to a depth of 700 Km where they end.Hollow Planet Seismology vs Solid Earth Seismology – Jan Lamprecht
http://www.bibliotecapleyades.net/tierra_hueca/esp_tierra_hueca_9.htm?sa=X&ved=0CBgQ9QEwATgUahUKEwjg2ezcuvnGAhVDaxQKHdy4DesThe asthenosphere is the highly viscous, mechanically weak and ductilely deforming region of the upper mantle of the Earth.
It lies below the lithosphere, at depths between ≈80 and ≈200 km (≈ 50 and 124 miles) below the surface.
…
The asthenosphere is generally solid although some of its regions could be melted (e.g. below mid-ocean ridge).The lower boundary of the asthenosphere is not well defined.
The thickness of the asthenosphere depends mainly on the temperature.
For some regions, asthenosphere could extend as deep as 700 km (430 mi).
https://en.wikipedia.org/wiki/Asthenosphere
Source: US Geological Survey: http://earthquake.usgs.gov/earthquakes/search/
Therefore, it’s very possible The Ringing Wet Earth contains a Liesegang Cavity.



I do not have time to post the links now, but there is little doubt Earth accreted heterogenously from fresh supernova debris, beginning with the accretion of its iron core, probably when Fe-60 was still and decaying away.
Iron cores became accretion sites for stone meteorites that forms further from the Sun, lost momentum and fell toward the gravitational center of the Solar System – the pulsar that became the core of the current Sun.
Pingback: Liesegang Cavities: 5 – Antipodal Hotspot | MalagaBay
Pingback: Crowd Source Science: Dutchsinse | MalagaBay
Pingback: Supernova SN 185 | MalagaBay
Pingback: Eric Laithwaite: Inward Travelling Magnetic Field | MalagaBay
Pingback: Hollow Science | MalagaBay